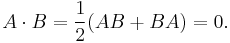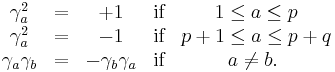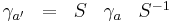Clifford module

In mathematics, a Clifford module is a representation of a Clifford algebra. In general a Clifford algebra C is a central simple algebra over some field extension L of the field K over which the quadratic form Q defining C is defined.

The abstract theory of Clifford modules was founded by a paper of M. F. Atiyah, R. Bott and A. Shapiro. A fundamental result on Clifford modules is that the Morita equivalence class of a Clifford algebra (the equivalence class of the category of Clifford modules over it) depends only on the signature 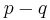p-q mod 8. This is an algebraic form of Bott periodicity.

Contents

Matrix representations of real Clifford algebras

We will need to study anticommuting matrices (AB = −BA) because in Clifford algebras orthogonal vectors anticommute

A \cdot B = \frac{1}{2}( AB %2B BA ) = 0.

For the real Clifford algebra 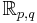\mathbb{R}_{p,q}\,, we need p + q mutually anticommuting matrices, of which p have +1 as square and q have −1 as square.

\begin{matrix} \gamma_a^2 &=& %2B1 &\mbox{if} &1 \le a \le p \\ \gamma_a^2 &=& -1 &\mbox{if} &p%2B1 \le a \le p%2Bq\\ \gamma_a \gamma_b &=& -\gamma_b \gamma_a &\mbox{if} &a \ne b. \ \\ \end{matrix}

Such a basis of gamma matrices is not unique. One can always obtain another set of gamma matrices satisfying the same Clifford algebra by means of a similarity transformation.

\begin{matrix} \gamma_{a'} &=& S &\gamma_{a } &S^{-1} \end{matrix}

where S is a non-singular matrix. The sets γ a' and γ a belong to the same equivalence class.

Real Clifford algebra R3,1

Developed by Ettore Majorana, this Clifford module enables the construction of a Dirac-like equation without complex numbers, and its elements are called Majorana spinors.

The four basis vectors are the three Pauli matrices and a fourth antihermitian matrix. The signature is (+++-). For the signatures (+---) and (---+) often used in physics, 4x4 complex matrices or 8x8 real matrices are needed.

See also

References